
A Teoria de Jogos e as Suas Aplicações
Fevereiro 10, 2022
A Teoria de Jogos é uma ferramenta matemática que modeliza as decisões em contexto de interação entre os agentes, isto é, contextos em que o resultado de cada escolha depende das escolhas feitas pelos outros, o que é uma visão muito realista. Por isso falamos de “jogos”, na medida em que a jogada/decisão/estratégia de um agente é determinada e confere valor não apenas por si, mas também pela jogada que induz no(s) outro(s) jogador(es), a qual, por sua vez, vai influenciar o resultado para esse agente. E por aí fora. E vice-versa. Trata-se de uma otimização condicionada, em que o conjunto de restrições leva em conta o comportamento esperado dos outros jogadores, a reação a esse comportamento esperado, a reação à reação, etc.
Assim, a Teoria de Jogos é útil para entender contextos de interdependência e interação. Podemos dar como exemplo os mercados, em que empresas rivais se inter-influenciam na escolha de estratégias de inovação, de marketing, de qualidade, de preço, de canais de distribuição, de responsabilidade social, etc., mas também situações de conflito armado ou guerras comerciais entre países, negociações diplomáticas, a preservação do ambiente, questões de ética, as relações familiares ou de vizinhança, as relações laborais, as relações entre o Governo e os cidadãos, leilões, a disputa eleitoral entre partidos políticos ou as coligações destes, a sobrevivência das espécies no mundo animal, e muito mais.
Foi no contexto económico, para mercados oligopolistas, que a Teoria de Jogos conheceu o seu grande desenvolvimento aplicado, passando da pura formulação matemática para a modelização de fenómenos do mundo real. Mercados oligopolistas são aqueles em que o número de empresas é suficientemente grande para haver interação (mais de uma, isto é, excluímos os monopólios, que têm solução unicamente determinada) e suficientemente pequeno para que as ações de cada uma contem (isto é, excluímos os mercados de concorrência perfeita, que também têm solução unicamente determinada). Podemos estudar rivalidade entre as empresas, através de jogos não cooperativos, ou cooperação, através de jogos cooperativos. Um conceito chave da teoria de jogos cooperativos é o conhecido valor de Shapley, que propõe dividir os ganhos de uma coligação pelos seus membros remunerando cada participante de acordo com o seu contributo marginal para a mesma. Embora o estudo da cooperação tenha sido o ponto de partida da Teoria de Jogos, foi o estudo da rivalidade que mais se desenvolveu, até porque um jogo cooperativo pode ser abordado como um jogo de negociação não cooperativo.
Qualquer jogo requer a definição de alguns elementos para a sua caracterização: quem são os jogadores, quais são as estratégias ao dispor de cada um, quais são os resultados (payoffs) associados a cada possívelcombinação de estratégias dos vários jogadores, quais são as regras do jogo (por exemplo, ordem das jogadas). Matematicamente, temos o conjunto J de jogadores J = {j1, j2,…, jn} (n≥2), sendo que para cada jogador i (i=1, …n) existe um conjunto Si de estratégias possíveis com pelo menos 2 elementos. O produto cartesiano S = S1 x S2 x … x Sn é o espaço de estratégias do jogo. Cada jogador i tem uma função de utilidade ui que associa um nível de satisfação (payoff) a cada perfil de estratégias em S.
Um pouco de História e alguns exemplos
Como marco histórico temos, entre outros, a publicação em 1944 da obra “Theory of games and economic bahavior” de John von Neumann (matemático) e Oskar Morgenstern (economista), que impulsionou o estudo dos jogos no ramo da Economia. Outro marco histórico de referência na Teoria de Jogos é a formalização do chamado “dilema do prisioneiro” por Albert Tucker em 1953, um jogo simples mas poderoso na sua capacidade de ilustrar situações em que o interesse individual, ao sobrepor-se ao interesse coletivo, conduz todos para um resultado pior, inclusive os jogadores que procuraram miopicamente garantir o melhor para si. Trata-se de um jogo extremamente útil para analisar, por exemplo, os atuais dilemas ambientais e climáticos. Sendo o ambiente um recurso comum, está sujeito à conhecida “tragédia dos comuns”, em que o interesse individual leva à sobre-exploração do recurso e, no limite, à sua extinção.
Noutra aplicação muito atual, o “dilema do prisioneiro” pode facilmente usar-se para modelizar a decisão individual de uso de máscara ou de vacinação em contexto de pandemia: para cada jogador individualmente pode ser mais compensador não usar máscara e/ou não se vacinar, desde que os outros o façam (um típico problema de free-riding), o que levará a um resultado eventualmente pior para todos, em que ninguém usa máscara nem se vacina. Por isso, pode competir às autoridades (que, em última análise, intervêm nas regras de alguns jogos) ajustar os payoffs através de prémios ou penalizações (como por exemplo não poder aceder a eventos culturais ou frequentar restaurantes), de forma a levar o resultado do jogo para a combinação cooperativa em que a sociedade como um todo fica melhor. Dito por outras palavras, colocar os incentivos certos para que as externalidades sejam internalizadas. Num contexto mais global, o “dilema do prisioneiro” pode igualmente aplicar-se à distribuição das vacinas contra a covid-19 a nível mundial.
Foi também no início dos anos 50 que surgiu a enorme contribuição do matemático John Nash, prémio Nobel da Economia em 1994 (juntamente com John Harsanyi e Reinhard Selten), com o seu conceito de equilíbrio. O equilíbrio de um jogo pode ser visto como a solução desse jogo, aquilo que podemos esperar que aconteça se os jogadores jogarem de acordo com os pressupostos. Nash definiu equilíbrio como o conjunto de estratégias tal que nenhum jogador pode melhorar a sua posição, dado o que os outros jogadores estão a jogar. Sendo isto válido para todos, nenhum jogador tem incentivo a jogar de forma diferente, logo estamos num equilíbrio. A esta situação chamamos equilíbrio de Nash:
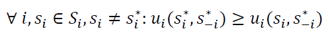 em que 𝑠*−𝑖 representa as jogadas ótimas dos outros n-1 jogadores, que não o jogador i.
em que 𝑠*−𝑖 representa as jogadas ótimas dos outros n-1 jogadores, que não o jogador i.Em certos jogos pode existir uma estratégia que é sempre a melhor resposta, qualquer que seja(m) a(s) jogada(s) do(s) rival(rivais). Neste caso falamos em estratégia dominante: esta é a que será sempre jogada, logo torna-se óbvia de prever se os jogadores jogarem de forma racional. O “dilema do prisioneiro” tem um equilíbrio em estratégias dominantes, que é cada um prosseguir o seu bem individual, sem olhar ao bem coletivo. Um equilíbrio em estratégias dominantes é um equilíbrio de Nash, mas nem todos os equilíbrios de Nash são equilíbrios em estratégias dominantes. Quando existe uma estratégia dominante, as restantes são estratégias dominadas e nunca serão escolhidas por um jogador racional.
Preferências diferentes
A hipótese da racionalidade é um pressuposto da Teoria de Jogos clássica que tem merecido algumas críticas. Assumir que os jogadores se comportam sempre de maneira racional pode ser demasiado exigente, na medida em que existem por vezes comportamentos impulsivos, para não falar em aditivos. Como assumir racionalidade para um jogador alcoólico ou viciado em substâncias? A resposta está nas preferências. A Teoria de Jogos dá a solução do jogo para uma determinada estrutura de preferências e para um jogador viciado em substâncias a otimização das suas preferências está em consumir.
Dada a estrutura de preferências do jogador (sejam elas quais forem), uma irracionalidade aparente pode consistir em jogar estratégias fora do equilíbrio, de forma a forçar o rival a uma estratégia também fora do equilíbrio, mas que leva o primeiro jogador para uma solução melhor. Esta irracionalidade é apenas aparente, na medida em que, de forma inteligente, explora os incentivos dados pelas combinações de payoffs e proporciona uma melhoria de posição.
A hipótese de que cada jogador quer obter o melhor payoff possível para si próprio é por vezes vista como excluindo comportamentos altruístas e, por essa via, falhando em captar toda a realidade. Porém, não é necessariamente assim, uma vez que o payoff corresponde à satisfação retirada ou, na nomenclatura das escolhas individuais, à utilidade do jogador. Se um jogador for altruísta, a sua função de utilidade incorporará o bem-estar do(s) outro(s) e a maximização da utilidade terá esse bem-estar em conta, tal como sucede se, ao contrário, o jogador tiver como objetivo aniquilar o seu rival.
Estratégias puras e mistas
Um jogador joga uma estratégia pura quando escolhe essa estratégia com probabilidade 1 (e todas as outras com probabilidade zero). No entanto, pode admitir-se que o equilíbrio consiste não em jogar uma estratégia com toda a certeza, mas em atribuir probabilidades às várias estratégias possíveis, considerando que o jogador escolhe cada uma delas com uma certa probabilidade, como se jogasse aleatoriamente (o que por vezes é conotado com fazer bluff). Ou seja, admitimos que o jogador escolhe uma distribuição de probabilidade sobre as estratégias puras. Neste caso estamos perante um equilíbrio em estratégias mistas.
Por exemplo, antecipando que os condutores conduzem com nível excessivo de alcoolémia x% das vezes, a polícia monta uma operação stop com y% de probabilidade; e vice-versa, ou seja, antecipando que a polícia faz uma operação stop com y% de probabilidade, os condutores irão beber demais x% das vezes. Estamos neste caso perante um equilíbrio de Nash em estratégias mistas: dada a probabilidade atribuída ao comportamento do(s) outro(s) jogador(es), cada um escolhe a melhor combinação de probabilidades para si. Esta otimalidade recíproca (“algo e vice-versa”) faz com que ninguém tenha incentivo a alterar a sua decisão, logo estamos em equilíbrio.
Podemos facilmente imaginar exemplos análogos ao anterior em contexto de pandemia: prevendo que se formem ajuntamentos com probabilidade α, ou que os cidadãos não usem máscara com probabilidade β (o que pode entender-se como cada cidadão usar máscara (1-β)% das vezes, ou como (1-β)% dos cidadãos usarem sempre e os restantes nunca), as autoridades irão decidir agravar as medidas (por exemplo com confinamento ou recolher obrigatório) com probabilidade γ; reciprocamente, prevendo um agravamento das medidas com probabilidade γ, os cidadãos têm como comportamento ótimo para eles não usar máscara com β% de probabilidade ou formar ajuntamentos com α% de probabilidade. Para ilustrar, imaginemos o seguinte jogo, em que não agravar as medidas quando há ajuntamentos tem um custo máximo para a autoridade (por exemplo em termos de reputação); por outro lado, agravar as medidas tem um custo (por exemplo devido a redução de receitas fiscais) que é maior quando mesmo assim não se consegue evitar os ajuntamentos. Os cidadãos preferem sempre que não haja agravamento das medidas; não havendo(havendo) agravamento das medidas, o bem estar para os cidadãos é superior quando fazem(não fazem) ajuntamentos. Nenhum dos lados sabe o que o outro vai fazer, mas atribui as probabilidades α e γ constantes da tabela. O primeiro payoff apresentado em cada célula é o payoff dos cidadãos. Com estes payoffs, e igualando para cada jogador o valor esperado das duas decisões possíveis para gerar aleatoriedade, no equilíbrio em estratégias mistas existe uma probabilidade fifty-fifty de as autoridades agravarem as medidas e, perante isso, os cidadãos vão fazer ajuntamentos 5/7=71% das vezes, o que, por seu lado, leva as autoridades a terem como ótimas as probabilidades 50%-50%. Naturalmente, se os payoffs não forem estes, as probabilidades também serão diferentes.

Um resultado importante da Teoria de Jogos, provado em pouco mais de uma página (Nash, 1950), é que para um jogo com um número finito de jogadores e estratégias existe sempre equilíbrio de Nash, pelo menos em estratégias mistas.
Alguns jogos têm multiplicidade de equilíbrios, o que coloca o problema de seleção, ou seja, torna-se difícil prever o que irá suceder. Por exemplo, na criação de uma plataforma digital para aproveitar economias de rede, um equilíbrio possível é a plataforma não chegar a existir por falta de número suficiente de adesões pelo menos por um dos lados do mercado, mas outro equilíbrio é ela “arrancar” e tornar-se gigante, como algumas que conhecemos. Para jogos com multiplicidade de equilíbrios, Harsanyi (1995) propôs o conceito de Nash equilibrium with the highest theoretical probability, que consiste em avaliar a força do incentivo que seria necessário dar a cada jogador para ele escolher uma determinada estratégia.
Diferentes tipos de jogos: de soma constante ou não, simultâneos ou sequenciais, repetidos ou não, com uma ou mais variáveis estratégicas
Embora a análise da Teoria de Jogos tenha começado com jogos de dois jogadores e de soma zero, o equilíbrio de Nash permite a análise de jogos com n jogadores, de soma nula ou não. Jogos de soma nula são aqueles em que, seja qual for a combinação de estratégias, o que um jogador ganha é o que o outro perde, de tal forma que o somatório dos payoffs é sempre zero. Pode pensar-se numa guerra: se um dos lados ganha, o outro perde. Ou num jogo de xadrez: se um jogador ganha, o outro perde.
Podemos também considerar jogos de soma constante, mas não nula; por exemplo, num torneio de xadrez existe normalmente 1 ponto para distribuir pelos 2 jogadores em cada jogo: o que ganhar recebe 1 ponto, o outro recebe 0 e se empatarem cada um recebe 0.5, ou seja, trata-se de um jogo de soma constante igual a 1.
Muitos jogos da vida real, porém, não têm soma constante, seja ela zero ou outra: por exemplo, num duelo entre duas rivais da tecnologia em que ambas estão a decidir se devem ou não inovar no seu produto, a soma dos payoffs será certamente diferente caso ambas inovem ou caso nenhuma inove; mesmo se uma inovar e a outra não, a soma dos payoffs pode ser diferente consoante aquela que inovar, pois nada obriga a que os jogadores sejam “simétricos”, isto é, tenham as mesmas características por exemplo em termos de eficiência produtiva (fator do lado da oferta) ou de reputação no mercado (fator do lado da procura). O mais realista será mesmo considerar jogadores “assimétricos”.
No que diz respeito às regras do jogo, uma distinção básica é entre jogos simultâneos (representados em forma de matriz) e jogos sequenciais (representados em forma de árvore). No segundo tipo os jogadores decidem sequencialmente, por uma ordem especificada; existe, pois, a possibilidade de observar a(s) escolha(s) do rival ou rivais antes de decidir (como num jogo de xadrez). Nos jogos sequenciais pode existir first-mover advantage, quando a escolha do primeiro a jogar consegue condicionar de tal forma a escolha do seguinte que leva o jogo para o resultado desejado pelo primeiro, second-mover advantage, quando existe benefício por exemplo em copiar o comportamento do outro (o que pode suceder em processos de inovação ou de transferência de tecnologia), ou nenhuma delas. O conceito de equilíbrio utilizado para encontrar a solução em jogos sequenciais é o de equilíbrio de Nash perfeito nos subjogos (subgame perfect Nash equilibrium).
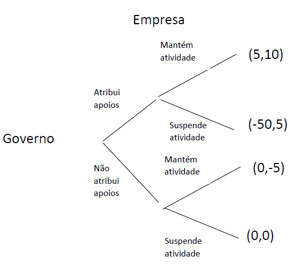
Como exemplo consideremos mais um jogo “pandémico” simples, em que o Governo de um país tem de decidir se atribui ou não apoios às empresas que decidam suspender a sua atividade durante a pandemia, e estas, observando a decisão do Governo, decidem então manter-se em atividade ou suspender. A árvore seguinte representa uma versão possível deste jogo, em que o primeiro payoff apresentado para cada combinação de estratégias é o payoff do primeiro jogador. Conceder apoios tem um custo para o Governo (-50), mas, se a empresa se mantiver em atividade, esse custo pode ser compensado com receitas fiscais (atuais ou futuras, se pensarmos que ajuda a que a economia não contraia tanto). Se a empresa receber apoios, prefere manter-se em atividade (10>5), se não receber prefere suspender (-5<0). Antecipando isto, a decisão racional do Governo é conceder os apoios.
Em jogos sequenciais o conjunto de informação disponível aquando da jogada pode ser mais ou menos vasto e tem de ser definido. A informação tem valor. No conjunto de jogos de informação imperfeita merecem destaque os jogos de sinalização, em que um jogador tenta passar ao outro informação sobre si próprio, construindo uma reputação à medida que o jogo se desenrola. Podemos dar como exemplos a reputação de oferecer um produto com muito boa qualidade, ou a reputação de ser bom pagador da dívida contraída. O equilíbrio de Nash utilizado nestes jogos é o equilíbrio bayesiano perfeito, em que as probabilidades a priori vão sendo atualizadas com recurso à regra de Bayes.
Por oposição aos jogos sequenciais, nos jogos simultâneos não existe de todo a possibilidade de observar o comportamento do adversário; note-se que para tal não é estritamente necessário que os jogadores decidam todos ao mesmo tempo, bastando que decidam no desconhecimento da decisão do(s) outro(s), com base em expetativas sobre o que ele(s) irá(irão) fazer. Matematicamente, estabelece-se uma função de reação ou função melhor resposta, que especifica, para cada jogada do adversário, a decisão ótima a tomar. Facilmente se intui que o equilíbrio de Nash estará na interseção das funções de reação (solução de um sistema de equações), quando as expetativas estão corretas e se verificam.
Alguns jogos são jogados uma só vez, outros são repetidos. Por exemplo, empresas que concorrem num mesmo mercado não tomam apenas uma vez a decisão sobre qual o preço a praticar, mas vão ajustando consoante as condições de mercado. A repetição do jogo tende a aumentar a probabilidade de se chegar a um equilíbrio cooperativo, em que a “maldição” do dilema do prisioneiro é ultrapassada, pois todos percebem que têm mais a ganhar em cooperarem. Além disso, a repetição permite a introdução de penalizações ou de prémios, o que também aumenta o incentivo a cooperar, sobretudo se o jogo for “infinitamente repetido”, isto é, se não tiver um fim à vista, pré-estabelecido.
Na vida real os jogadores têm frequentemente de tomar decisões que envolvem mais do que uma variável. Por exemplo, na gestão de uma pandemia o Governo tem de decidir se fecha as escolas, se reduz o período de isolamento, se torna o uso de máscara obrigatório em espaços fechados, etc. A escolha de mais do que uma variável é modelizada através de jogos em estádios. Assim, podemos ter jogos em que num primeiro estádio as empresas escolhem por exemplo o investimento em inovação e no segundo estádio concorrem entre si em quantidades no mercado do produto.
A Teoria de Jogos e os dilemas sociais
Embora o dilema do prisioneiro capte muitos dilemas sociais, nem toda a interação social se resume a dilemas do prisoneiro. Há muitos mais dilemas sociais e há jogos em que o “bom” equilíbrio coexiste com o “mau”, isto é, ambos são possíveis, tal como há jogos em que o “bom” equilíbrio prevalece. Por exemplo, haverá uma franca recuperação económica para um país que consiga controlar a pandemia? Se o resto do mundo também tiver conseguido controlá-la, a resposta será provavelmente sim, e estaremos no “bom” equilíbrio. Mas se o resto do mundo não tiver conseguido, das duas uma: ou o país se fecha para manter esse controlo mas perde receitas turísticas e outras vantagens da abertura, ou desiste do controlo para supostamente manter a economia a funcionar. Imaginemos dois jogos que podem representar estes dilemas e vejamos como têm resultados diferentes:
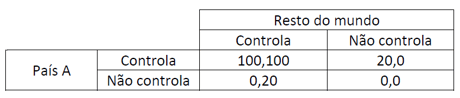
Nesta matriz os payoffs do status-quo (não controlo) estão normalizados a zero. Se a pandemia for controlada em todo o mundo, o resultado é de 100 para ambos os jogadores; se só o país A a controlar o seu ganho é menor, de apenas 20. Pode ver-se que o equilíbrio único deste jogo é todos fazerem um esforço no sentido de controlar a pandemia: controlar é estratégia dominante para todos.
No entanto, se admitirmos que o controlo isolado tem custos muito elevados a nível da atividade económica, que não compensam se o controlo não for global, podemos modelizar essa alteração com a seguinte mudança da matriz (se preferirmos, em vez de Resto do mundo podemos pensar num país B geograficamente próximo de A):
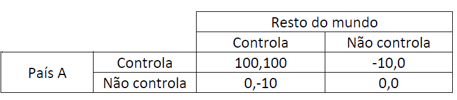
Com esta mudança passam a existir dois equilíbrios de Nash, um em que a pandemia é controlada em todo o mundo e outro em que não é (repare-se que se o resto do mundo não controlar, para o país A o melhor é também não controlar e vice-versa).
Para finalizar note-se que, tal como qualquer modelização, os jogos são necessariamente uma representação simplificada das múltiplas combinações e permutações que a realidade nos oferece. A Teoria de Jogos ajuda a prever o comportamento dos agentes e a clarificar situações de interação social, permitindo isolar efeitos e entender como é que certos resultados inesperados podem de facto acontecer.
Referências
Harsanyi, J. and R. Selten (1988). A General Theory of Equilibrium Selection in Games, Cambridge, Massachusetts: MIT-Press.
Harsanyi, J. (1995). A new theory of equilibrium selection for games with complete information. Games and Economic Behavior 8(1), 91-122.
Nash, J. (1950). Equilibrium points in n-person games. Proceedings of the National Academy of the USA 36(1):48-49. https://doi.org/10.1073/pnas.36.1.48
Von Neumann, J. and O. Morgenstern (1944). Theory of Games and Economic Behavior, Princeton University Press.
O curso de Economia para Engenheiros oferecido pelo Técnico+ fornece ferramentas teóricas para melhor entender os fenómenos económicos, suas causas e impactos, com aplicações ao caso português. Como analisar, por exemplo:
- As repercussões do atual contexto pandémico nos mercados à luz da Microeconomia e da Macroeconomia?
- Que deslocações provoca na procura e na oferta, no equilíbrio dos mercados, e como é que as estruturas de custos, as elasticidades e o grau de concorrência influenciam esses efeitos?
- Que políticas macroeconómicas podem ser usadas num contexto de recessão e qual o papel dos estabilizadores automáticos?
- O que é o crescimento económico, como se mede e como se relaciona com o desemprego e com a inflação?
- Qual a importância da poupança e do investimento?
- Como flutuam estas variáveis ao longo do ciclo económico, como pode o Estado promover a estabilização da economia, quais os níveis e o racional para a intervenção do Estado, em que consiste o Orçamento de Estado e a Balança de Pagamentos, quais os instrumentos que Portugal tem num contexto de moeda única europeia, como vão a Comissão Europeia e o Banco Central Europeu atuar e ajudar à recuperação económica da economia europeia e dos países europeus que pertencem à União Europeia e à zona euro (como é o nosso caso)?
A estas e outras perguntas se pretende dar resposta, a partir dos conceitos económicos fundamentais e da sua aplicação quer à economia portuguesa quer à União Europeia e à zona euro em que estamos inseridos, permitindo uma análise rigorosa dos efeitos em causa e um olhar crítico sobre a informação transmitida nos jornais económicos nacionais e internacionais. Este curso constitui uma importante mais-valia para os participantes, ajudando a melhor entender o ambiente económico em que se insere a sua organização.

Margarida Catalão Lopes
Professora Associada no Instituto Superior Técnico, no Departamento de Engenharia e Gestão. É participante em projetos de investigação nacionais, sendo a sua principal área de investigação a Economia Industrial e a Teoria de Jogos. Foi Economista Sénior e coordenadora do Grupo de Sistema Bancário do Departamento de Estudos do Banco de Portugal, e consultora da Autoridade da Concorrência. É Agregada pelo Instituto Superior de Economia e Gestão e Doutora, Mestre e Licenciada em Economia pela Faculdade de Economia da Universidade Nova de Lisboa (NOVASBE). É também autora de vários artigos de investigação publicados em revistas científicas internacionais, livros e capítulos de livros.
Related Posts
Prev
Next
Categorias:
- AGILE (2)
- agileleadership (1)
- Antenas (1)
- Arquitetura Empresarial (1)
- Blockchain (3)
- carro (1)
- Cibersegurança (9)
- Ciência de Dados (6)
- Cloud (1)
- Corporate Innovation (1)
- cursos (1)
- Data Analytics (3)
- Design Thinking (1)
- Digital Innovation Leadership (2)
- Economia (2)
- Economia Circular (5)
- Educação (5)
- Empreendedorismo e Inovação (5)
- Engenharia e Gestão (15)
- Escola de Outono (1)
- Eventos (7)
- Finanças para Engenheiros (1)
- Formação Avançada (9)
- Future IT Leadership (2)
- Gestão de Operações (1)
- hidrogenio (1)
- Informação e Sistemas Empresariais (6)
- Informática (17)
- Inovação (3)
- inteligência artificial (2)
- Inteligência Artificial Generativa (4)
- Laboratório (1)
- Lean Six Sigma (3)
- Liderança (1)
- Machine Learning (1)
- Parcerias (22)
- Reabilitação Urbana (2)
- Redes (1)
- RFID (1)
- Sistemas (2)
- Sustentabilidade (3)
- Tecnologia (5)
- Telecomunicações e 5G (1)
- Transformação Digital (4)
- Técnico+ (7)
Subscreva a nossa newsletter
Receba informações sobre cursos, artigos e eventos do Técnico+
Artigos recentes



.jpg)
